制作芝诺悖论短视频体会芝诺教你如何一本正经地胡说八道——理解“芝诺悖论”

用户投稿 2025年08月18日 16:25:02 34 0

芝诺教你如何一本正经地胡说八道——理解“芝诺悖论”

不得不承认，哲学是由“空话”和“瞎话”组成的。说它是“空话”，是因为哲学中的概念和观点都是虚无的、与现实生活没有直接关系的，哲学知识没有现实的功利意义；说它是“瞎话”，是因为有些哲学结论很明显地与经验和常识相违背。

第一个“睁眼说瞎话”的哲学家或许就是古希腊哲学家巴门尼德。

他有两个非常有意思的观点：首先，他认为只有我们的思维世界是真实的，而丰富多彩的大千世界只是梦幻泡影，是感官对我们的一种欺骗。（这类似于佛教的态度，当然二者背后的道理是不同的）。其次，他认为所有运动变化的现象是不存在的，也是一种感观层面的幻觉，真正的存在物是不变化的，世界是绝对静止的。总之，他很不信任感性经验，认为和严密的逻辑理性相比，前者更容易出错。既然如此，我们就不能依靠感觉，而只能凭借理性去认识世界。而且，当感觉和思维发生了分歧的时候，我们应该毫不犹豫地站在后者的立场上去否定前者。

他提出了这两个很违反感觉常识的观点，但却对具体的解释不感兴趣。于是，论证这两个奇葩观点的任务就交给了他的弟子——芝诺。我们今天就来看看芝诺是怎样用哲学的方法来“忽悠”我们的。

提到芝诺，你或许听过所谓的“芝诺悖论”，芝诺提出过很多匪夷所思的案例，比如“阿喀琉斯追不上乌龟”“飞矢不动”等，这些都属于芝诺悖论，我也曾写过关于这两个案例的文字（有兴趣的同学可以点击文后的链接阅读相关文章），但是我们今天想从哲学史的角度来重新理解芝诺。

我们刚才说道芝诺提出悖论都是为了论证他的老师巴门尼德的两个奇葩观点。他的思路很简单，就是让感觉和理性发生冲突，这些冲突就被称为“悖论”。在这些冲突中，我们会发现感觉现象有目共睹，但是理性逻辑更是不容置疑，在这种纠结中我们只好最终选择理性思维——因为感觉可能会出错，但是思维却显得那么无懈可击。

我们先看他是怎样论证“运动变化是虚假的”这个观点的。

其实刚才提到的“阿喀琉斯追不上乌龟”、“飞矢不动”的悖论就是为了论证这个观点而提出的。因为之前写过，这里就不再赘述。在这里补充一个类似的悖论，那就是“二分法”：

假设一个人要从A点行进到B点，那么它当然要先到达A、B两点之间的中点；要想从这个中点到达B，又要先到达这两点之间的中点……剩下的路程可以无限划分，也就是说有无数个“中点”，而他要想到达目的地，每次都要先到达剩余路程的中点，于是他永远也无法到达终点！

这样一来，理性思维（运动者永远到不了终点）和常识（运动者可以到达）就发生了矛盾，这时芝诺会怂恿我们支持前者，让我们抛弃感觉，相信理性。最终信服他老师的结论：运动变化是不存在的、是假象，真实的世界是静止不动的。

接下来，该论证“现实世界是虚假的”这个观点了。巴门尼德认为真正存在的事物只有一个，它是一个整块，它只存在于我们的脑海中。我们平时接触的看似形形色色的的、独立存在的事物都是假的，比如我眼前的杯子、桌上的手机、头上戴的耳机，这些都是假的。世界没有这么复杂、这么花哨。

芝诺把我们的常识归纳为“存在是‘多’”这样一个观点，意思就是“存在物是丰富多样的”，他的目的就是推翻这个观点，他用的方法是归谬法。

首先，他假设“存在是‘多’”是正确的。如果是这样，那么就有两种可能情况：存在物或者是无限的多，或者是有限的多。

如果存在物是无限多的，那么又会有两种情况：它们或者是有体积的，或者是无体积的。

如果这些存在物是有体积的，那么它们的整体加在一起就是无限大的，但是一个无限大的事物对于古希腊人而言是无法用思维把握的，所以他们就认为不可能有这么一个东西！这个可能性就这么被简单粗暴地pass掉了。

如果这些存在物是无体积的，那么整个存在加起来也就是无体积的，那么我们也可以说它是无限小的。一个物体既是无限小的，也是无限大的，这也超出了古希腊人的有限的理解力，他们认为这样的东西不存在，于是这条也pass掉。

无限多的两种情况都排除了，现在就剩下“有限多”的情况了。这种情况又可以分为两类：这些有限的存在物自身或者是连续的，或者是间断的。

就第一种情况而言，虽然每一个存在物自身是连续的，但是因为存在物是“多”，所以存在物之间还是间断的、有空隙的，这些空隙中还可以塞进无限多个更小的存在物。这样一来，存在物就又成无限多了！

就第二种情况而言，如果存在物自身内部是间断的，那么这些存在物本身就可以（在它们的间断处）分成许多更小的存在物，这样就又成无限的了。

所以最后的结论是，真正地存在物既不是有限的“多”，也不是无限的“多”，而是一个浑然的整体，是一个“一”！所以我们平时看到的看似独立存在的、形形色色的东西都是假的！

我相信，很少有人愿意耐心地听他一板一眼地以分类讨论和反证的方法花式胡扯（如果不是要写这篇文章，我也不愿意替他这样睁眼说瞎话）。

表面上看，这一通忽悠既无聊又漏洞百出。但是芝诺和他老师的良苦用心其实是很深刻的。

由于绝大部分时间是凭借常识生活的，我们很少会怀疑亲眼见到的东西，正所谓“眼见为实”，这样固然有效降低了犯错的几率，提高了工作和生活的效率。但是如果只生活在感觉经验中，我们的想象力和理性就永远没有开发的可能，我们和那些匍匐在大地上的动物就不会有本质的区别。

芝诺要做的，就是动摇我们对经验的信念，为我们认识世界多增加一个角度，告诉我们理性和感觉都是认识世界的方法。只不过他采取了一种矫枉过正的策略：否定感觉，只承认理性（这就是所谓的“形而上学”）。

站在经验的立场上，要驳倒他很容易：芝诺说一个人永远也到不了目的地，难道他一辈子都大门不出，二门不迈吗？当然不是，他一生遍游希腊各城邦；他又说我们看到的东西都是假的，难道他一辈子清心寡欲、隐居山林了吗？正好相反，他一生积极参与城邦事务，跟他有关或无关的事他管了个遍。

可能你会说，这不就结了吗？他已经用自己的行动反驳了自己，这证明他自己都不相信自己那一套。

当然，他不相信，而且我们也相信他不相信。

芝诺是一个正常人

可是哲学家们是一群生活在理论中的物种，经验或行动层面的攻讦对他们是无效的。他们会告诉你：“经验的那一套准则我当然知道，有种用理性给我挑刺。”

所以哲学是什么？它或许就是一种严肃的思维游戏。说它是游戏，因为我们无法在真实生活中拿它当真；说它严肃，因为它总能给我们一些意味深长的启发，让我们学会接纳和理解。

相关文章链接：芝诺悖论怎么破？

智慧笔记：芝诺悖论——竟以“极限”之名令辩证法熠熠生辉？

作者|公子小白

【愿哲学被听见】公子小白继续和您一同寻找西方哲学的踪迹。

哲学家芝诺

芝诺是巴门尼德的学生，他的鼎盛时期大约在公元前468年前后。芝诺曾经就伊奥尼亚学派有关变化的世界本源观念，提出了举世闻名的四个著名论证。但事实上，芝诺的观点因过度极端，与其说是对其恩师巴门尼德思想的延续，倒不如说，芝诺旨在维护巴门尼德有关真理学说的层面上，采用了矫枉过正的做法。

柏拉图的注说

沉思的芝诺

后来，在柏拉图所著的《巴门尼德篇》中，曾经指出，他们采用了“以彼之道，还施彼身”的辩护策略：有的人指责说，倘若“存在是不变的一”予以承认，那么，所得出的荒谬结论必然是“事物不能运动”；此时，他们则反驳，如果对存在之变化予以承认，如此一来，事物不能运动的结论同样以此推到而出，并且，这将成为矛盾与前提的悖论，岂不是更加荒谬？

芝诺悖论

1.二分法：

二分法悖论

任何运动的事物，早在其抵达目的地之前，需要事先完成它的全程；在达到1/2之前，需要事先完成其1/2；在达到其1/4之前，则事先完成其1/4……。如此无限分割，直至无穷，因此它将无限趋近于目的地却始终难以达到目的地。

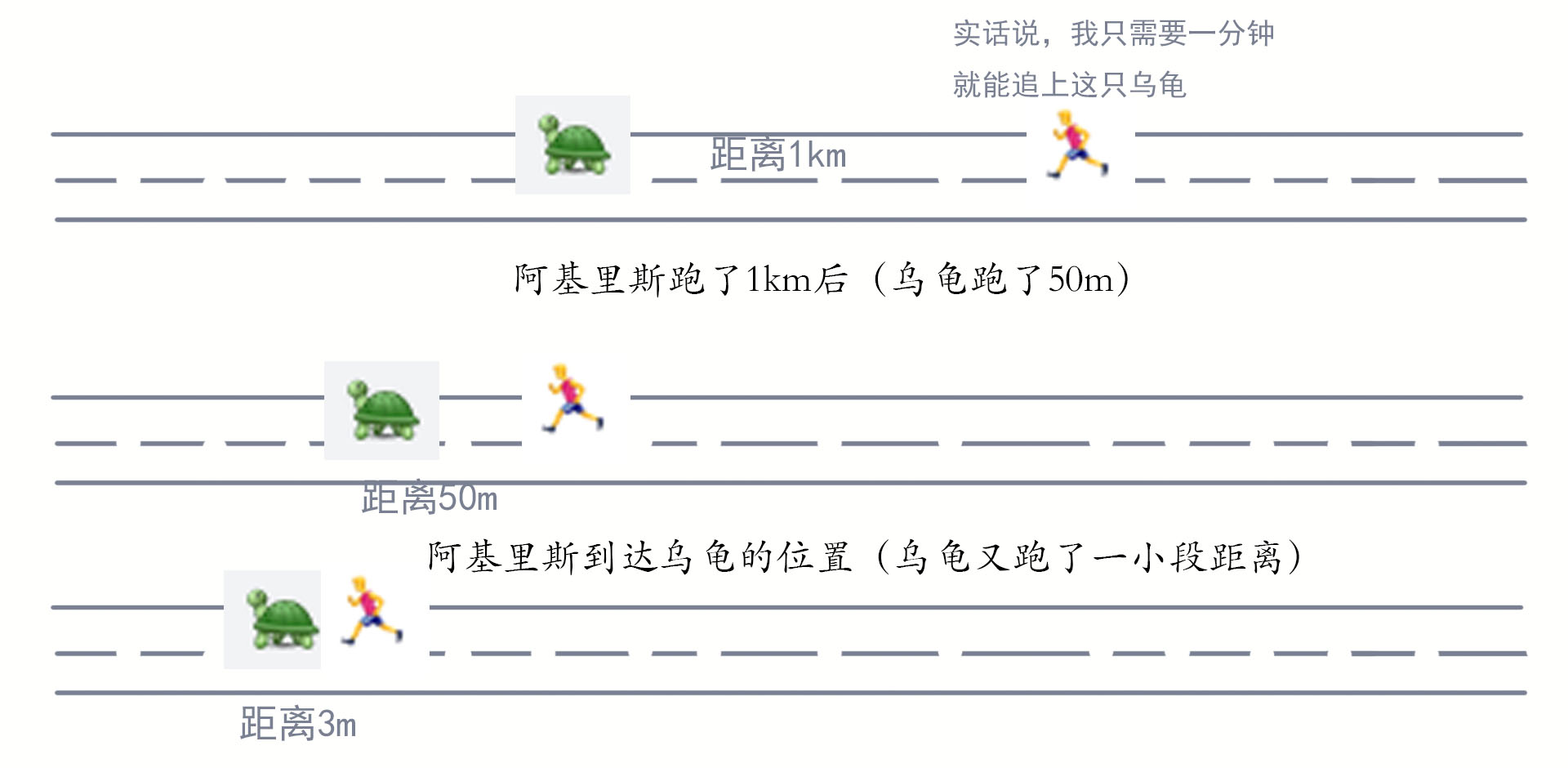
2.阿基里与乌龟赛跑：

阿基里与乌龟赛跑

我们假设古代奥林匹克赛跑冠军阿基里与一只乌龟进行一场赛跑比赛，乌龟首先爬行了一段路程；当阿基里开始起步并同样跑完这段路程之后，乌龟又再次向前爬行一段路程；当阿基里跑完这有一段路程后，乌龟又再一次向前爬行了一段路程；如此一来，一爬以追，无限往复，赛跑冠军将永远不可能追上这只缓慢爬行的乌龟。这则阿基里与乌龟赛跑的悖论向人们证明，运动着的事物并无快慢可言。

3.飞矢不动：

飞矢不动

我们想象一下，一个飞矢在一段时间内所飞过的路程，其中可以被切割成无数个时刻或瞬间。而在每一个瞬间，飞矢都占据着一个孤立的位置，那么，在每一个位置上的飞矢则是静止不动的。换句话说，飞矢实际上是驻留在整个路程的每一个不同的位置之上，而非从一个位置飞到另外一个位置。

4.一倍的时间等于一半的时间：

一倍的时间等于一半的时间悖论

如上图↑，我们来假设B和C两组系列字母所运动的速度相同且方向相反，A、B、C三组系列字母的每个部分的大小、质量都完全相同。那么，B4抵达A4的时间，则势必与C1抵达A1的时间相同。

但是，由于相对于A系列字幕，B系列字幕仅仅移动了两格，因此其运动时间则是相较于C系列字幕运动时间的一半。也就是说，C系列字幕相对于B系列字幕移动了四格，所以C系列字母运动的时间要足足比B系列字母的运动时间多出了一倍。这么一来，本应相等的时间却出现了倍数的差别，这便是“一倍时间等于一半时间”的悖论。

无穷

在芝诺的四个悖论中，除了第四个“一倍时间等于一半时间”悖论外，其他三个悖论的内容均适用于收敛数列。因此，“二分法”可以以现代数学符号表示为1，1/2，1/4，1/8，1/2n（n趋向无穷大）的数列。

对芝诺悖论的评价

尽管通过现代数学的论证不难解释芝诺所提出的上述悖论的谬误，但他们绝不仅仅是简单意义上的“诡辩”，其后蕴藏着的哲学意义形成了对后世的巨大启示。可以说，芝诺通过有关运动的数学分析，历史性地使用了微积分运算，并将其见诸在“极限”的概念之上，也正是对“极限”的使用，承认了无限与有限，连续与间断的相互统一。而以上这些，都是数学所无法予以正面的证明和解答的。“极限”作为数学领域最基础的概念，却不能被数学本身加以解释，需要进一步诉诸更为严谨的现代逻辑与数学哲学。